第１２回授業の準備【参考】：場合の数　Q124〜137

【Q1】　A，B，C，D，Eの5人が一列に並ぶと，並び方は全部で何通りあるか。
【A】120通り

【Q2】　男A，B，C，D，E，女G，F，Hの中から男3人，女2人を選ぶとき，選び方は全部で何通りあるか。
【A】30通り

【Q3】　図の３×４の方眼紙の中に大小いくつの正方形があるか。
【A】20個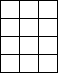　　　

【Q4】　3人でジャンケンを1回だけして，1人だけ勝つ場合は何通りあるか。
【A】9通り

【Q5】　床に図のようなタイルをおき，アからオを赤，青，緑の3色で同じ色を使ってもよいが隣は違う色にして色分けする。色分けする方法は全部で何通りあるか。
【A】12通り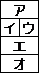　　　

【Q6】　1つの長いすにA，B，C，Dの4人が座るとき，BとDがとなりあわない座り方は全部で何通りあるか。
【A】12通り

【Q7】　図において左下のAからBを通って右上のCに行く最短経路は何通りあるか。
【A】12通り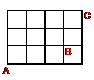　　　

【Q8】　A，B，C，D，Eの5人が1つの輪をつくるとき，並び方は全部で何通りか。
【A】24通り

【Q9】　長さが1cm，2cm，4cm，5cm，7cmの棒が1本ずつあり，この中から3本を使って三角形を作るとき，全部で何種類の三角形を作ることができるか。
【A】2種類

【戻る】　 【ホーム】