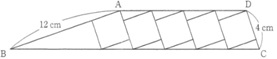
【問47】 図のように、同じ大きさの正方形5個を並べ、両端の正方形の一辺を延長した直線と各正方形の頂点を通る直線を結んで台形ABCDを作ったところ、辺ABの長さは12cm、辺CDの長さは4cmとなった。
このとき、台形ABCDの面積は正方形1個の面積の何倍となるか。【2013国家一般職】
1 7倍
2 7.5倍
3 8倍
4 8.5倍
5 9倍
【解説】 【問47】 DCに平行なAからACへの交点をEとし△ABEを考える。
正方形の一辺の長さをXとすると,12:4=(12−X):Xとなり
これからXを求めるとX=3となる。 正方形面積は9
正方形以外の面積は1/2(3×9)+1/2(1×3)×9=27
正方形が5個だから45 ∴8倍
【答】 3
【補講】
どこに注目するか。繰返しは特徴部分のみ考慮。
Aの三角形から糸口を見出す。
三角形の面積や長さでは,相似比を利用することがよくあるので,マスターすべし
