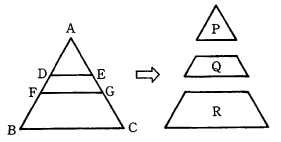
【問】 図のように正三角形ABCをBCに平行な2直線DE,FGで切って,P,Q,Rという3つの図形をつくった。P,Q,Rの面積の比が4:5:16であるとき,周の長さの比はいくらか。(p.104_No.148**)
1 4:5:16
2 5:6:10
3 6:7:12
4 7:9:14
5 8:10:15
【答】 3
【解説】
△ADE:△AFG:△ABC=4:9:25
面積だから長さは2:3:5
PQRそれぞれの長さを求める。P=6,Q=1×2+2+3=7,R=2×2+3+5=12
|
No.60 面積比 29BS7_10 【KW】 正三角形 平行 図形 面積 【問】 図のように正三角形ABCをBCに平行な2直線DE,FGで切って,P,Q,Rという3つの図形をつくった。P,Q,Rの面積の比が4:5:16であるとき,周の長さの比はいくらか。(p.104_No.148**)  1 4:5:16 2 5:6:10 3 6:7:12 4 7:9:14 5 8:10:15 【答】 3 【解説】 △ADE:△AFG:△ABC=4:9:25 面積だから長さは2:3:5 PQRそれぞれの長さを求める。P=6,Q=1×2+2+3=7,R=2×2+3+5=12 |