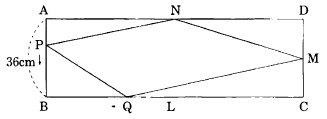
【問】 下図のように,長方形ABCDにおいて,辺ABの長さを36cm,辺BC,CD,DAの中点をそれぞれL,M,Nとする。点Aから点Bに向かって秒速1cmで移動する点Pと,点Lから点Bに向かって秒速2cmで移動する点Qが同時に出発するとき,四角形PQMNの面積が最大になるのは出発してから何秒後か。ただし,辺BCの長さは辺ABの長さの4倍より大きい。【地上14年度】299_12**
|
1 9秒後 2 12秒後 3 15秒後 4 18秒後 5 21秒後 |
 |
【答】 1
【解説】
|
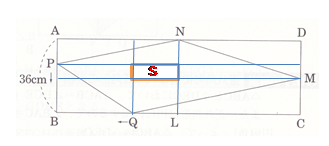
四角形□PQMNの面積は,□ABCDから真ん中の□Sを除いた半分に□Sを足した値である。 □ABCDの横幅をaとすると,t秒後の位置から関係式を作る。 Sは,S=2t×(18−t)=36t−2t2 □PQMN=(36a−S)÷2+S Sを代入 (36a−(36t−2t2 ))÷2+(36t−2t2 )=18a−18t+t2+36t−2t2 =−t2 +18t+18a ⇒ 最大値は−2t+18=0のtだから,t=9(秒) |
 |