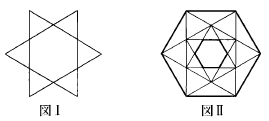
【問】 図Ⅰは,1辺の長さが等しい2つの正三角形を,重心を中心として60°回転させて重ねたものである。この図形の隣り合う各頂点を直線で結び,さらに,内側の正六角形の頂点を1つおきに結ぶと,図Ⅱで示される図形となる。このとき,図Ⅱにおいて,一番外側にできた正六角形の面積は,一番内側にできた正六角形の面積の何倍か。 【国税専門16年度】293_3*
|
1 6倍 2 4√3 倍 3 6√2 倍 4 9倍 5 6√3 倍 |
 |
【答】 4
【解説】
|
相似な図形の面積は1辺の長さの自乗に比例する。 一番小さな正六角形の1辺の3倍が外側の大きな正六角形であるから,9倍となる。 |
 |