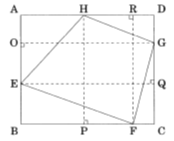
【問】 次の図のような,辺AB=13cm,辺BC=16cmとする長方形ABCDと,辺AB,辺BC,辺CD,辺AD上の点E,点F,点G,点Hで囲まれた四角形EFGHがある。今,点E,点F,点G,点Hから辺CD,辺AD,辺AB,辺BCに垂線を引き,それぞれの交点をQ,R,O,Pとすると,EO=5cm,FP=6cmとなった。このとき,四角形EFGHの面積はどれか。【特別区26年】297_8**
|
1 104 cm2 2 119 cm2 3 124 cm2 4 134 cm2 5 144 cm2 |
 |
【答】 2
【解説】 BH48と同
|
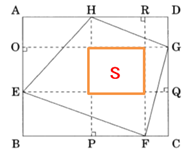
図のSの部分を除くと四角形EFGHの面積は全体の面積の半分である。 Sは,S=5×6=30 だから,(13×16−30)÷2=89 これにSを加えるとよいから,から,89+30=119 が得られる。 |
 |