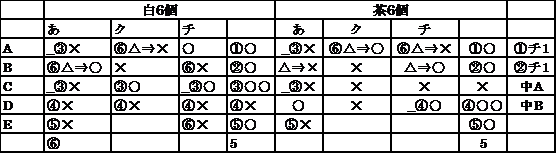亂栤亃丂 敀怓偲拑怓偺偍搚嶻偺閈摢偑6屄偢偮寁12屄偁傝丆敀怓偲拑怓偺偄偢傟偵傕丆彫摛擖傝丆僋儕乕儉擖傝丆僠儑僐擖傝偺镼偑2屄偢偮偁偭偨丅A乣E偺5恖偑2屄偢偮怘傋偰師偺傛偆側敪尵傪偟偰偄傞偲偒丆巆偭偨2屄偺閈摢偵偮偄偰妋幚偵偄偊傞偺偼偳傟偐丅丂亂崙嘦2008亃76Q25
丂A丗乽暿乆偺怓偺閈摢傪怘傋偨偲偙傠丆偦偺堦偮偼僠儑僐镼偱偁偭偨丅乿
丂B丗乽暿乆偺怓偺閈摢傪怘傋偨偲偙傠丆偦偺堦偮偼僠儑僐镼偱丆傕偆堦偮偺拞恎偼A偲偼堘偭偰偄偨乿
丂C丗乽敀怓偺閈摢傪2偮怘傋偨偲偙傠丆拞恎偺慻崌偣偑A偲堦抳偟偰偍傝丆偦偺堦偮偼僋儕乕儉镼偱偁偭偨v
丂D丗乽拑怓偺閈摢傪2偮怘傋偨偲偙傠丆拞恎偺慻崌偣偑B偲堦抳偟偰偄偨v
丂E丗乽暿乆偺怓偺閈摢傪怘傋偨偲偙傠丆拞恎傕暿乆偱丆敀怓偺閈摢偼A偑怘傋偨拑怓偺閈摢偲拞恎偑堦抳偟偰偄偨v
侾丂敀怓偱彫摛镼偲敀怓偱僋儕乕儉镼丂丂
俀丂拑怓偱僋儕乕儉镼偲拑怓偱僠儑僐镼丂
俁丂敀怓偱彫摛镼偲拑怓偱僋儕乕儉镼丂丂
係丂敀怓偱僋儕乕儉镼偲拑怓偱彫摛镼丂丂
俆丂敀怓偱僠儑僐镼偲拑怓偱彫摛埞
亂摎亃俁
亂夝愢亃
丂 昞偵彂偒崬傫偱偄偔丅
丂彫摛佀偁丆僋儕乕儉佀僋丆僠儑僐佀僠
嘆A偐傜敀拑偵乑丆僠儑僐1
嘇B偐傜敀拑偵乑丆堦偮偼僠儑僐
嘊C偐傜敀2偱僋儕乕儉仜丆拞恎偑A偲堦抳偩偐傜A偲C偼僠儑僐偲僋儕乕儉丆彫摛偼側偟
嘋D偐傜拑2偱丆拞恎偺慻崌偣偑B偲堦抳偩偐傜堦偮偼嘇偐傜僠儑僐仜丆僋儕乕儉側偟
嘍E偐傜敀拑偵乑丆嘊偐傜A偵彫摛偑側偄偐傜E傕彫摛偼側偄
嘐偙偙偱巆傝偺昞傪杽傔傞丅敀拑偦傟偧傟6屄偱奺怓1屄偢偮梋偭偰偄傞偐傜丆巿1丆2偼側偟
丂敀偺僠儑僐偼2屄偑寛傑偭偰偄傞偐傜巆傝偼亊丅敀偺B偼彫摛偲側傝丆僠儑僐偼拑偲側傞
丂峏偵丆晄柧側仮偑杽傑傞丅敀偺彫摛偑寛傑傞偲慖戰巿3偺傒偑彫摛偱惓夝偲側傞丅
丂