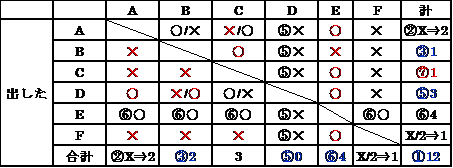
亂栤亃丂 椃峴愭偱弌夛偭偨A乣F偺6恖偑丆屳偄偺楢棈愭傪岎姺偟丆椃峴屻偵庤巻偺傗傝偲傝傪偟偨丅師偺偙偲偑暘偐偭偰偄傞偲偒丆妋幚偵偄偊傞偺偼偳傟偐丅(崙嘦2011)102Q35
丂嘆丂6恖偑弌偟偨庤巻偺憤悢偼12捠偱丆1恖偑摨偠幰偵2捠弌偡偙偲偼側偐偭偨丅
丂嘇丂A偑庤巻傪弌偟偨恖悢偲傕傜偭偨恖悢偼摨偠偩偭偨丅
丂嘊丂B偼1恖偵庤巻傪弌偟丆2恖偐傜庤巻傪傕傜偭偨丅
丂嘋丂B偑庤巻傪弌偟偨幰偼丆B埲奜偵傕2恖偐傜庤巻傪傕傜偭偨丅
丂嘍丂D偼3恖偵庤巻傪弌偟偨偑丆扤偐傜傕庤巻傪傕傜傢側偐偭偨丅
丂嘐丂E偼庤巻傪弌偟偨恖悢丆傕傜偭偨恖悢偲傕4恖偩偭偨丅
丂嘑丂F偼庤巻傪弌偟偨恖悢丆傕傜偭偨恖悢偲傕A偺敿悢偩偭偨丅
侾丂A偼B偵庤巻傪弌偟偨丅丂丂
俀丂B偼D偐傜庤巻傪傕傜偭偨丅丂丂
俁丂C偼F偐傜庤巻傪傕傜偭偨丅丂丂
係丂D偼A偵庤巻傪弌偟偨丅丂丂
俆丂F偼D偐傜庤巻傪傕傜偭偨丅
亂摎亃係
亂夝愢亃
丂 丂専摙偺弴斣偲偟偰丆昞傪嶌傝忣曬傪彂偒擖傟傞丅
丂嘆偐傜崌寁偺壓偵12婰嵹
丂嘇偐傜A偺寁偵傂偲傑偢X偲抲偔丅
丂嘊偐傜寁偲崌寁棑偵婰嵹
丂嘋曐棷
丂嘍D偺庴偗偼0偐傜俢偺廲偑杽傑傞丅
丂嘐E偑弌偟偨偺偼D埲奜偺4恖偱杽傑傞丅
丂嘑寁偑12偱丆BDE偱8偩偐傜巆傝4丆X偼嬼悢偩偐傜X偼2偱丆C偑弌偟偨1偲寛傑傞丅
丂嘋偐傜B偑弌偟偨偺偼ACE偺壜擻惈偑偁傞偑丆B埲奜偵2恖偐傜傕傜偭偰偄傞偐傜寁3捠庴偗偰偄傞丅ACE偱3捠偼C偺傒偱偁傞丅E偺庴偗4捠偑寛傑傞丅C偑弌偟偨1捠傕妋掕
F偑弌偟偨1捠傕妋掕丆A偑庴偗偰2捠傕妋掕
C偺庴偗偼E埲奜側偄丅F偑庴偗偨偺傕E埲奜偵側偄丅
D偑弌偟偨偺偼巆傝偺ABE丆B偑庴偗偨偺偼DE偱妋掕偩偐傜懠偼側偟丅
巆傝傕寁偲偺娭學偱杽傑傞丅