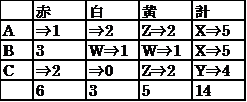【問】 A〜Cの3人が花屋で買ったチューリップの色と数について,次のア〜カのことが分かっているとき確実にいえるのはどれか。(特別区2006)148Q0
ア:3人が買ったチューリップの合計数は,赤色が6本,白色が3本,黄色が5本であった。
イ:AとBがそれぞれ買ったチューリップの数は,同数であった。
ウ:AとCがそれぞれ買った黄色のチューリップの数は,同数であった。
エ:Bが買った白色と黄色のチューリップの数は,同数であった。
オ:Cが買ったチューリップの数は,3人の中で最も少なかった。
カ:3人のうち2人は赤色,白色,黄色の3種類のチューリップを買い,他の1人は2種類の色のチューリップだけを買った。
1 Aが買った赤色のチューリップの数は,1本であった。
2 Aが買った白色のチューリップの数は,1本であった。
3 Bが買った赤色のチューリップの数は,1本であった。
4 Cが買った赤色のチューリップの数は,1本であった。
5 Cが買った白色のチューリップの数は,1本であった。
【答】1
【解説】
Bの黄は1又は3であり,3とすると白はBだけが買ったこととなり,他の2人とも2種類になりカの条件に合わない。
ゆえに,Wは1である。またZは2となる。オの条件から,計の欄のYは偶数であり,2,4が該当するが,2であればCは赤白が0になるから,カの条件に反する。
よって,Yは4である。同時にXが5も判明する。またBの欄の赤も3と分かる。1箇所が0であるから,残り4箇所を順に0と仮定して確認する。
赤Aが0だと,赤Cが3でCの合計4と矛盾。白Aを0とすると赤A3で赤Cも0で2か所0で矛盾。
赤Cが0だと同様に白Aが0で矛盾。残った白Cが0だと,白Aが2,赤Cが2,赤Aが1で全て条件を満たす。